常见的分布式并行策略

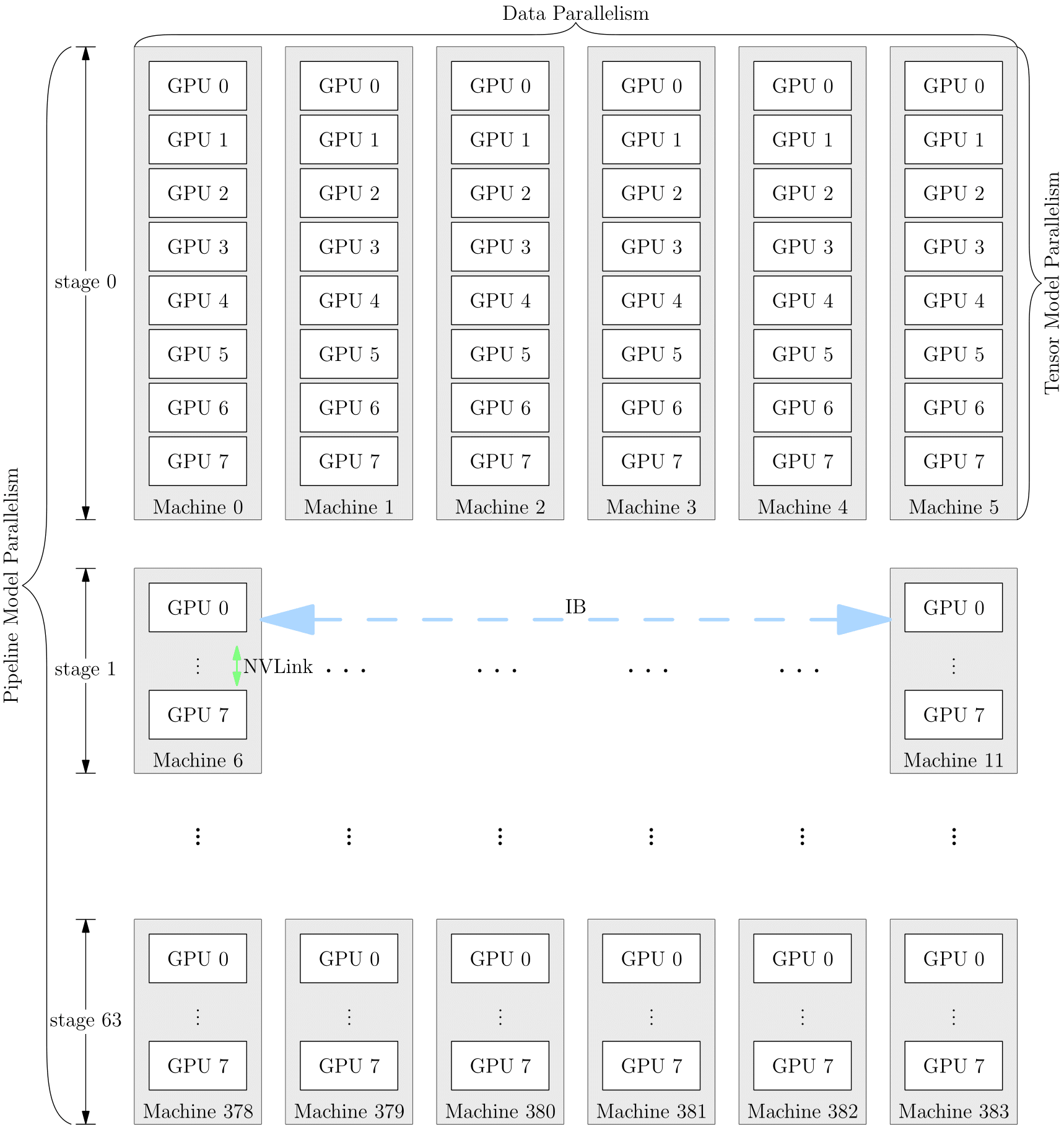
近年来，随着模型规模的不断扩大，训练一个单独的模型所需要的算力和内存要求也越来越高。然而，由于内存墙的存在，单一设备的算力以及容量受到限制，而芯片的发展却难以跟上模型扩大的速度。为了解决算力增速不足的问题，人们开始考虑使用多节点集群进行分布式训练，以提升算力。

数据并行

数据并行是将数据分为若干份，分别映射到不同的处理机中，每一台处理机上的模型是完整的、一致的，每一台处理机对数据执行相同的操作。根据不同问题，通过选择适用的并行算法可减少处理机之间的通信量，提升处理性能。

当一块 GPU 可以存下整个模型的时候，可以采用数据并行的方式获得更加准确的梯度，同时还可以加速训练。当数据集较大，模型较小的时候，由于反向过程中为同步梯度产生的通信代价较小，这时选择数据并行一般比较有优势。

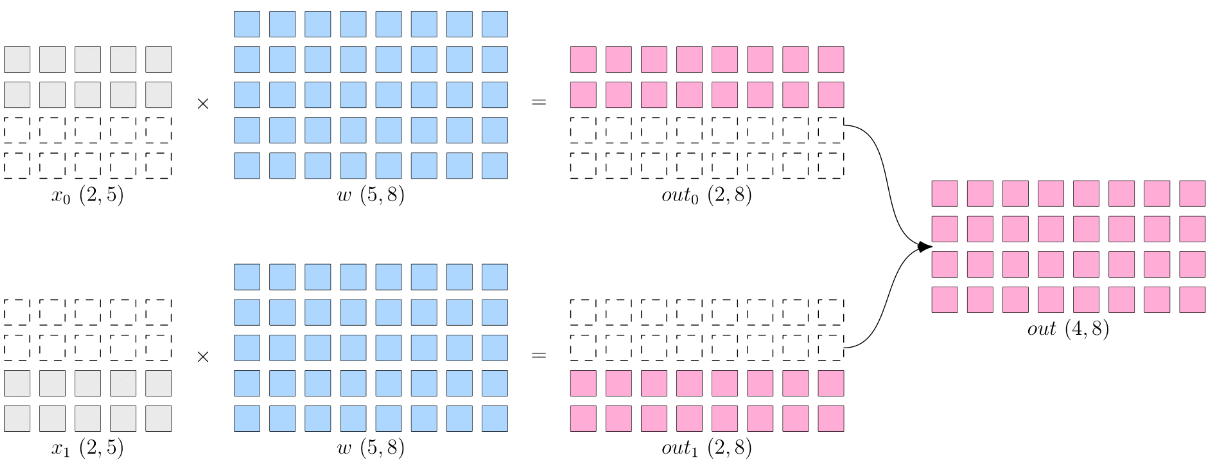
数据并行步骤：

输入数据切分数据并行运行过程中，会通过两种方式切分数据。
- 在每个 epoch 开始之前，将整个训练数据集根据并行进程数进行划分，无需进行数据通信，每个进程只读取自身划分到的数据；
- 数据读取由进程负责，数据读取后根据并行进程数切分，再发送到对应的进程中；
模型参数同步数据并行过程中，需要在处理数据时保持模型参数同步。模型参数同步可以在初始时使用相同的随机种子完成，以相同的顺序进行初始化来实现；也可以通过某一进程初始化全部模型参数后，向其他进程广播模型参数，实现同步。

训练过程中的每一个 step 都会更新模型参数，每个进程处理不同的数据会得到不同的 loss，由 loss 计算反向梯度并更新模型参数后，如何保证进程间模型参数正确同步，是数据并行需要解决的最主要问题。在反向传播的过程中，每个进程上的 loss 不同，因此每个进程在反向传播中会计算出不同的梯度。这时一个关键的操作是要在后续的更新步骤之前，对所有进程上的梯度进行同步，保证后续更新步骤中每个进程使用相同的全局梯度更新模型参数。由 AllReduce 对各个设备上的梯度进行同步，以确保各个设备上的模型始终保持一致。

假设一个 batch 有 n 个样本，一共有 k 个 GPU，第 j 个 GPU 分到 \(m_j\) 个样本，考虑等分的情况， \(m_j=\frac n k\) ，如果考虑总损失函数 loss 对参数 \(w\) 求导，则有：
\[\begin{aligned} \frac{\partial Loss}{\partial w} &= \frac{1}{n} \sum_{i=1}^n \frac{\partial l(x_i, y_i)}{\partial w} \\&= \frac{m_1}{n}\frac{\partial [\frac{1}{m_1} \sum_{i=1}^{m_1}l(x_i, y_i)]}{\partial w} + \frac{m_2}{n} \frac{\partial \frac{1}{m_2} \sum_{i=m_1+1}^{m_2}l(x_i,y_i)}{\partial w} + \dots \\&= \frac{m_1}{n} \frac{\partial l_1}{\partial w} + \frac{m_2}{n} \frac{\partial l_2}{\partial w} + \dots + \frac{m_k}{n} \frac{\partial l_k}{\partial w} \\&= \frac{1}{k}[\frac{\partial l_1}{\partial w} + \frac{\partial l_2}{\partial w} + \dots + \frac{\partial l_k}{\partial w}] \end{aligned}\]
可以看出，所有卡上总 batch 的平均梯度，和单卡上 mini-batch 的平均梯度汇总之后再平均的结果是一样的。
参数更新数据并行的参数更新是在输入数据切分和模型参数同步的步骤完成后进行的，得到相同的全局梯度之后，各自独立地完成参数更新。更新前，每个进程的参数相同；更新时，基于所有进程上的梯度同步得到的全局梯度也相同，所以实现在更新后每个进程得到的参数也是相同的。

数据并行 DP(Data Parallel)

单进程，多线程实现，每台机器有独立的模型。在 pytorch 中，使用 DataParallel:

model = nn.DataParallel(model, device_ids=[args.gpu])

Pytorch 的 DataParallel 复制一个网络到多个 cuda 设备，然后再 split 一个 batch 的 data 到多个 cuda 设备，通过这种并行计算的方式解决了 batch 很大的问题，但也有自身的不足：

单进程多线程，无法在多个节点上工作，不支持分布式，并且不支持使用 Apex 进行混合精度训练。同时它基于多线程的方式，受限于 Python 的 GIL，会带来性能开销，不适合用于计算密集型任务。
存在效率问题，主卡性能和通信开销容易成为瓶颈，GPU 利用率通常很低。数据集需要先拷贝到主进程，然后再 split 到每个设备上，权重参数只在主卡上更新，需要每次迭代前向所有设备做一次同步，每次迭代的网络输出需要 gather 到主卡上，主卡的负载和通信开销都很大。
不支持模型并行

分布式数据并行 DDP(Distributed Data Parallel)

多进程实现，不同步所有参数，同步梯度的误差。

model = nn.parallel.DistributedDataParallel(model, device_ids=[args.gpu])

Pytorch 的 Distributed DataParallel 中每个 GPU 都由一个进程控制，这些 GPU 可以都在同一个节点上，也可以分布在多个节点上。每个进程都执行相同的任务，并且每个进程都与所有其他进程通信。GPU 之间只传递梯度。

Pytorch 通过 distributed.init_process_group 函数初始化进程组来实现多进程同步通信。它需要知道 rank0 的位置，以便所有进程都可以同步，还需要知道预期的进程总数 world_size。每个进程都需要知道进程总数以及其在进程组中的顺序，以及使用哪个 GPU。model=DDP(model) 会把 parameter，buffer 从主节点传到其它节点，在每个进程上创建模型，DDP 通过这一步保证所有进程的初始状态一致，所有需要保证在这一步之后，不再修改模型的任何东西。torch.utils.data.DistributedSampler 可用来为各个进程切分数据，以保证训练数据不重叠（实际上就是 shuffle 数据集之后，把数据集依次分配给不同的进程）。

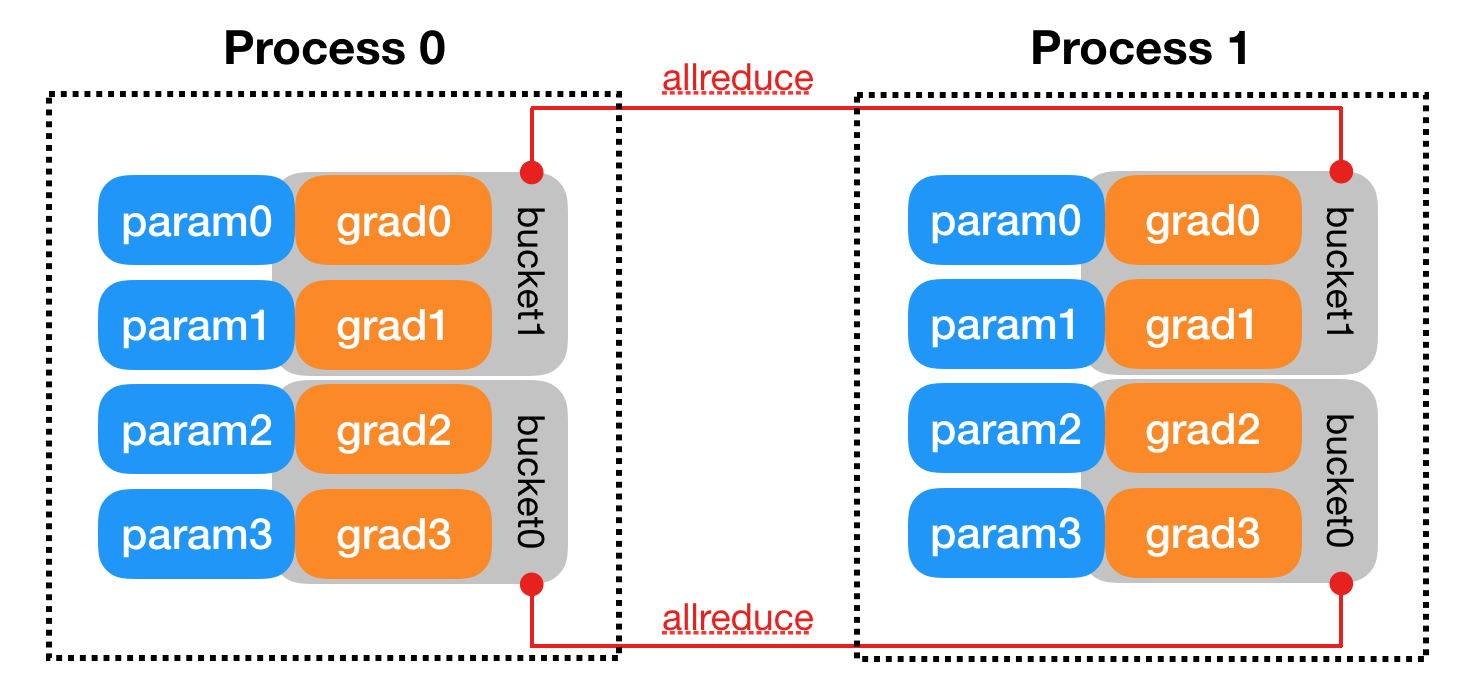
ddp_bwd_update

参数被分组，计算得到的梯度会马上进行通信，不必等待所有梯度计算结束再通信

将 rank = 0 进程中的模型参数广播到进程组中的其他进程，然后每个 DDP 进程都会创建一个 local reducer 来复制梯度同步。在训练过程中，每个进程从磁盘加载 batch 数据，并将它们传递到其 GPU。每个 GPU 都有自己的前向过程，完成前向传播后，梯度在各个 GPU 之间进行 all-reduce，每个 GPU 都收到其他 GPU 的梯度，从而可以独自进行反向传播和参数更新。同时，每一层的梯度不依赖于前一层，所以梯度的 all-reduce 和后向过程同时计算，以进一步缓解网络瓶颈。在后向过程的最后，每个节点都得到了平均梯度，这样各个 GPU 中的模型参数保持同步。

全切片数据并行 FSDP(Fully sharded data parallelism)

FSDP（Fully Sharded Data Parallel）是 Facebook AI Research (FAIR) Engineering 深度借鉴微软 ZeRO 之后提出的 PyTorch DDP 升级版本，可以认为是对标微软 ZeRO，其本质是 parameter sharding。Parameter sharding 就是把模型参数（使用 RPC）等切分到各个 GPU 之上，并且可以选择将部分训练计算卸载到 CPU。尽管参数被分片到不同的 GPU，每个 micro-batch 的数据对于每个 GPU worker 来说仍然是本地的。与 partition optimizer + gradient 相比，FSDP 在训练过程中通过通信的计算重叠对模型参数进行更均匀的切分，具有更好的性能。

FSDP 可以使用更少的 GPU 更有效地训练数量级更大的模型。FSDP 的关键是将 DDP 之中的 all reduce 操作分解为独立的 reduce-scatter 和 all-gather 操作。

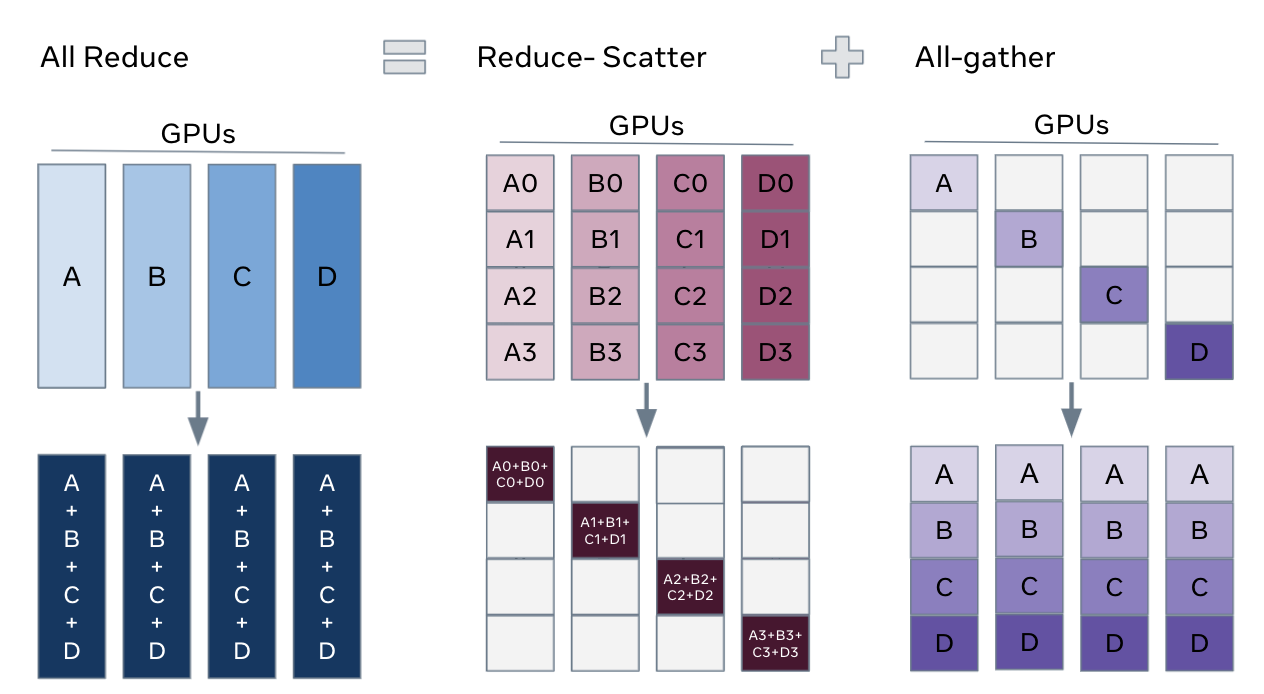
ar2rsag

reduce-scatter 阶段，在每个 GPU 上，会基于 rank 索引对 rank 相等的块进行 sum 求和；
all-gather 阶段，每个 GPU 上的聚合梯度分片可供所有 GPU 使用；

通过重排 reduce-scatter 和 all-gather，每个 DDP worker 只需要存储一个参数分片和优化器状态。

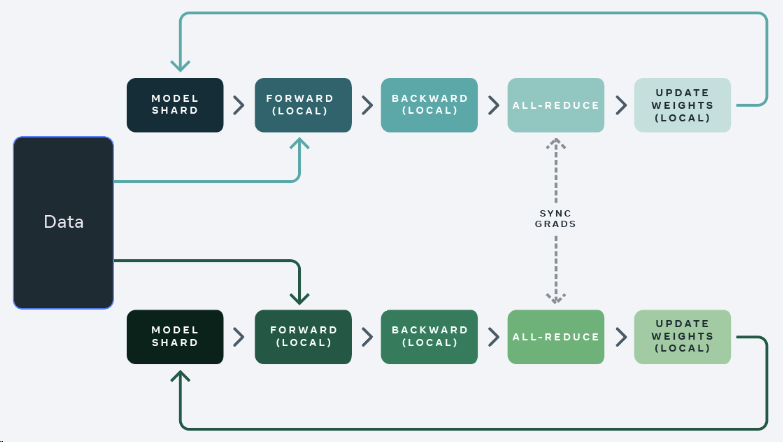
sharded_data_parallel_training

Sharded Data Parallel Training

fully_sharded_data_parallel_training

Fully Sharded Data Parallel Training

标准数据并行训练方法中，每个 GPU 上都存在模型的副本，forward 和 backward 只在自己的数据分片上运行。在执行完本地计算之后，每个本地进程的参数和优化器将与其它 GPU 共享，以计算全局权重更新；

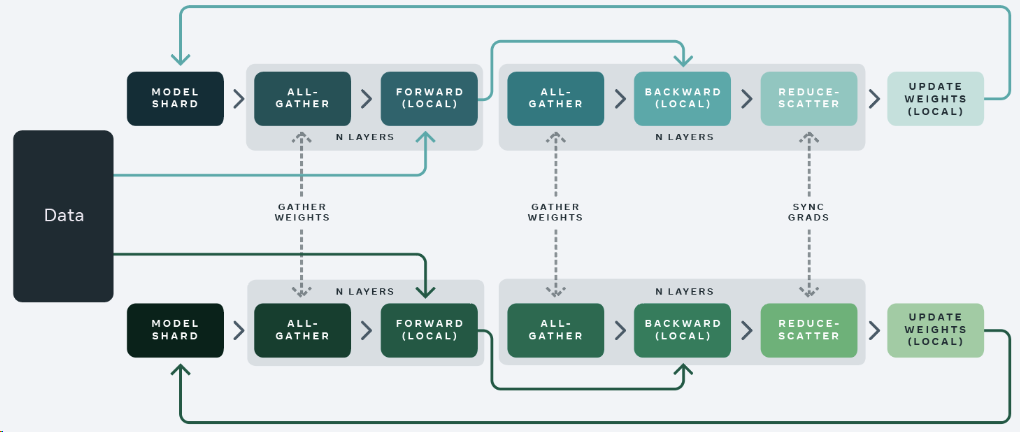
在 FSDP 中，每个 GPU 上仅存在模型的一个分片，每个 GPU 通过 all-gather 从其它 GPU 收集所有权重，用以进行前向计算，在反向传播之前再次执行权重收集，此时每个 GPU 上都是全部梯度，再执行反向传播操作，反向传播之后，局部梯度被聚合并且通过 reduce-scatter 在各个 GPU 上分片，每个分片上的梯度是聚合之后本分区对应的那部分。

为了最大限度提高内存效率，可以在每层前向传递之后丢弃全部权重，为后续层节省内存。

FSDP forward pass:
    for layer_i in layers:
        all-gather full weights for layer_i
        forward pass for layer_i
        discard full weights for layer_i

FSDP backward pass:
    for layer_i in layers:
        all-gather full weights for layer_i
        backward pass for layer_i
        discard full weights for layer_i
        reduce-scatter gradients for layer_i

可通过 Pytorch Lightning 使用 FSDP

model = MyModel()
trainer = Trainer(gpus=4, plugins='fsdp', precision=16)
trainer.fit(model)

trainer.test()
trainer.predict()

或者直接使用 FairScale 的 FSDP：

from fairscale.nn.data_parallel import FullyShardedDataParallel as FSDP
...
# sharded_module = DDP(my_module)
sharded_module = FSDP(my_module)
optim = torch.optim.Adam(sharded_module.parameters(), lr=0.0001)
for sample, label in dataload.next_batch:
  out = sharded_module(x=sample, y=3, z=torch.Tensor([1]))
  loss = criterion(out, label)
  loss.backward()
  optim.step()

模型并行

模型并行的本质是对计算资源进行分配。当神经网络非常大，数据并行同步梯度的代价就会很大，甚至模型过大无法直接被载入单个处理机中，这时，需要采用模型并行解决问题，将整个模型按层分解为多个模型，载入不同的处理节点分别进行计算。不同节点按照模型顺序进行排序，以流水线形式先后执行节点计算。

模型并行中，每个设备上的数据是完整的、一致的。但模型并行并非完全以并行方式完成，有时会以串行方式完成。

张量并行(Tensor Parallelism)

张量并行是指将张量沿特定维度分割成块，每个设备仅保存整个张量的一部分（intra-layer），同时不影响计算图的正确性。它涉及将算子的参数分发到不同的设备。然后，每个设备根据分配的数据片计算本地结果。最后，在算子计算结束时，插入集体通信（例如 all-gather 或 all-reduce）以获得最终结果。尽管有其优点，但张量并行性会带来更高的通信开销，因为每次分割张量操作后都需要同步通信。这种影响在跨节点训练期间尤其明显，低通信带宽会显着降低训练速度。

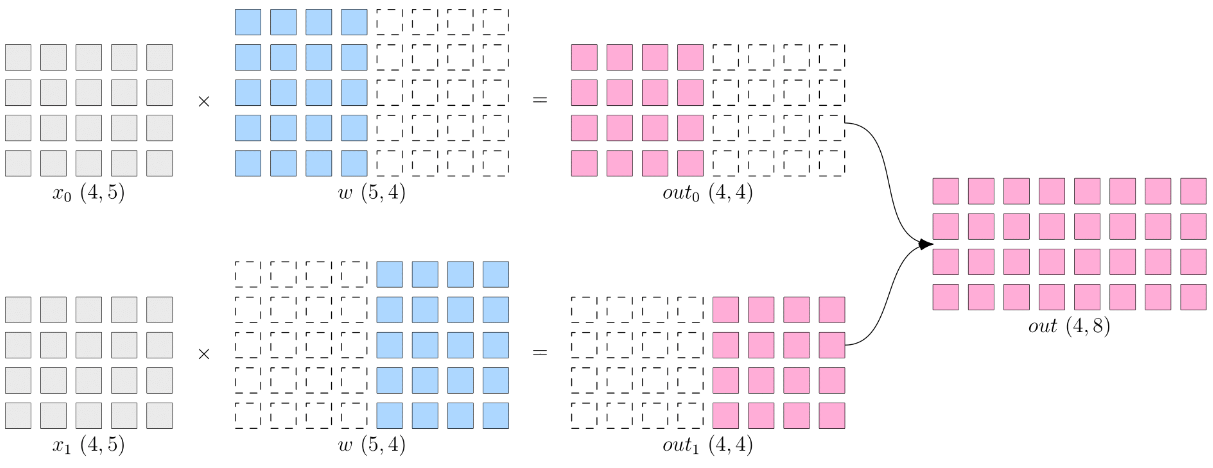
张量并行从数学原理上来看就是对于 linear 层把矩阵分块进行计算，对于非 linear 层不做额外设计。张量的切分方式分为按行切分和按列切分，分别对应行并行（将权重按行分块，输入按列分块，放到不同的 GPU 上计算）和列并行（将权重按列分块，输入按行分块，放到不同的 GPU 上计算）。

一维张量并行（Megatron）

目前最常用的是 1D 分片，将张量按照某一个维度进行划分（横着切或者竖着切）。目前，在基于 Transformer 架构的大模型中，最常见的张量并行方案由 Megatron-LM 提出，它是一种高效的 1D 张量并行实现，采用非常直接的张量并行方式，对权重进行划分后放至不同的 GPU 上进行计算。这种方法虽然将参数划分到多个 GPU 上，但每个 GPU 仍然需要存储整个中间激活，在处理大模型时会浪费大量显存空间。由于仅采用一维矩阵划分，在每次计算中，每个 GPU 都需要与其它 GPU 进行通信，因此，通信成本会随着并行度增高而激增。

多维张量并行（Colossal AI）

Colossal AI 提供多维张量并行，即以 2/2.5/3 维方式进行张量并行。

2D 张量并行

将 input 和 weight 都沿着两个维度均匀切分

在 Colossal-AI 中，2D 张量并行实现如下：

  import colossalai  
  import colossalai.nn as col_nn  
  import torch  
  from colossalai.utils import print_rank_0
  from colossalai.context import ParallelMode
  from colossalai.core import global_context as gpc
  from colossalai.utils import get_current_device

  # Parallel Config
  CONFIG = dict(parallel=dict(
      data=1,
      pipeline=1,
      tensor=dict(size=4, mode='2d'),
  ))

  parser = colossalai.get_default_parser()  
      colossalai.launch(config=CONFIG,  
      rank=args.rank,  
      world_size=args.world_size,  
      local_rank=args.local_rank,  
      host=args.host,  
      port=args.port)  
    
  class MLP(torch.nn.Module):  
      def __init__(self, dim: int = 256):  
          super().__init__()  
          intermediate_dim = dim * 4  
          self.dense_1 = col_nn.Linear(dim, intermediate_dim)  
          print_rank_0(f'Weight of the first linear layer: {self.dense_1.weight.shape}')  
          self.activation = torch.nn.GELU()  
          self.dense_2 = col_nn.Linear(intermediate_dim, dim)  
          print_rank_0(f'Weight of the second linear layer: {self.dense_2.weight.shape}')  
          self.dropout = col_nn.Dropout(0.1)  

      def forward(self, x):  
          x = self.dense_1(x)  
          print_rank_0(f'Output of the first linear layer: {x.shape}')  
          x = self.activation(x)  
          x = self.dense_2(x)  
          print_rank_0(f'Output of the second linear layer: {x.shape}')  
          x = self.dropout(x)  
          return x

  # build MLP
  m = MLP()

  # random input
  x = torch.randn((16, 256), device=get_current_device())

  # partition input
  torch.distributed.broadcast(x, src=0)
  x = torch.chunk(x, 2, dim=0)[gpc.get_local_rank(ParallelMode.PARALLEL_2D_COL)]
  x = torch.chunk(x, 2, dim=-1)[gpc.get_local_rank(ParallelMode.PARALLEL_2D_ROW)]
  print_rank_0(f'Input: {x.shape}')

  x = m(x)

2.5D 张量并行

与一维张量并行相比，二维张量并行降低了内存成本，但可能引入更多的通信，2.5D 张量并行在 2D 的基础上使用更多的设备来减少通信。

  # parallel config
  CONFIG = dict(parallel=dict(  
      data=1,  
      pipeline=1,  
      tensor=dict(size=8, mode='2.5d', depth=2),  
  ))

  ...
    
  # build model
  m = MLP()

  # random input
  x = torch.randn((16, 256), device=get_current_device())

  # partition input  
  torch.distributed.broadcast(x, src=0)  
  x = torch.chunk(x, 2, dim=0)[gpc.get_local_rank(ParallelMode.PARALLEL_2P5D_DEP)]  
  x = torch.chunk(x, 2, dim=0)[gpc.get_local_rank(ParallelMode.PARALLEL_2P5D_COL)]  
  x = torch.chunk(x, 2, dim=-1)[gpc.get_local_rank(ParallelMode.PARALLEL_2P5D_ROW)]  
  print_rank_0(f'Input: {x.shape}')  
    
  x = m(x)

在 d = 1 时，这种并行模式可以退化成 2D 张量并行，在 d = q 时，它变成 3D 张量并行。

3D 张量并行

  # parallel config
  CONFIG = dict(parallel=dict(  
      data=1,  
      pipeline=1,  
      tensor=dict(size=8, mode='3d'),  
  ))

  ...
    
  # build model
  m = MLP()

  # random input
  x = torch.randn((16, 256), device=get_current_device())

  # partition input  
  torch.distributed.broadcast(x, src=0)  
  x = torch.chunk(x, 2, dim=0)[gpc.get_local_rank(ParallelMode.PARALLEL_3D_WEIGHT)]  
  x = torch.chunk(x, 2, dim=0)[gpc.get_local_rank(ParallelMode.PARALLEL_3D_INPUT)]  
  x = torch.chunk(x, 2, dim=-1)[gpc.get_local_rank(ParallelMode.PARALLEL_3D_OUTPUT)]  
  print_rank_0(f'Input: {x.shape}')  
    
  x = m(x)

流水并行(Pipeline Parallelism)

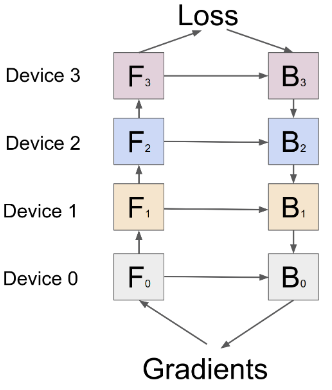
为了减少节点之间的通信量，提出了流水并行。流水并行性在层级别（inter-layer）对模型进行划分，同时还将 mini-batches 划分为 micro-batches。

朴素流水并行

朴素流水并行是实现流水并行最直接的方法。将模型按照 inter-layer 切分成多个部分（stage），并将每个部分（stage）分配给一个 GPU，然后对小批量数据进行常规训练，在模型切分成多个部分的边界进行通信。
```
  output = L4(L3(L2(L1(input))))
```
假设使用 K 块 GPU，朴素流水线的 Bubble 时间为 \(O(\frac{K-1}{K})\) ，当 K 越大，即 GPU 的数量越多时，空置的比例接近 1，即 GPU 的资源都被浪费掉了，因此，朴素流水线并行将会导致 GPU 使用率过低。另外，还需要加上在设备之间复制数据的通信开销，所以，4 张使用朴素流水线并行的 6GB 的卡能够容纳 1 张 24GB 卡相同大小的模型，而后者因为没有数据传输开销，训练得更快。
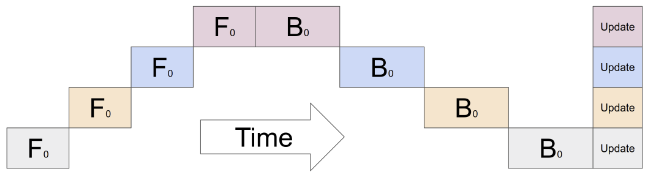
F-then-B 流水并行

先进行 forward 计算，将 forward 计算的中间结果都缓存下来，再使用缓存的结果进行 backward 计算。由于 F-then-B 缓存了多个 micro-batch 的中间变量和梯度，显存的实际利用率不高。

Bubble 时间为 \(O(\frac{K-1}{K+M-1})\) 。当 \(M \gg K\) 时，Bubble 时间可以忽略不计。
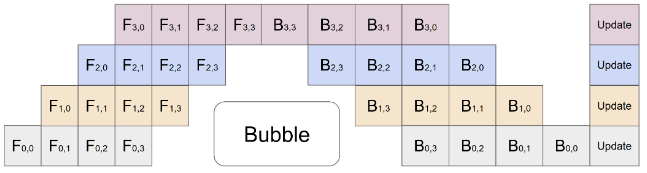
1F1B 流水并行

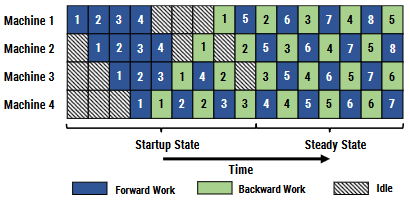
一个 stage 在做完一次 micro-batch 的 forward 之后，就立即进行 micro-batch 的 backward，然后释放资源，就可以让其它 stage 尽可能早开始计算。即把整体同步变成了众多小数据块上的异步，这些小数据块都是独立更新的。在 1F1B 的 steady 状态下，每台机器上严格交替进行前/后向计算，这样使得每个 GPU 上都会有一个 micro-batch 的数据正在被处理，从而保证资源的高利用率。

Bubble 时间为 \(O(\frac{K-1}{K+M-1})\) 。在设备显存一定的情况下，可以通过增大 M 的值（micro-batch的数量）来降低 bubble 率。

混合并行

混合并行，顾名思义，即将多种并行策略混用。下图展示的是 DP + TP + PP 混合并行。

Tags: MLSys Parallelism