自动微分在很多领域都被广泛使用，但直到深度学习出现时，才被用于计算机领域对程序做高效准确的求导。随着自动微分和其它微分技术的深入研究，其与编程语言、计算框架、编译器等领域的联系愈发紧密，并且衍生扩展出更通用的可微编程概念。

自动微分原理

微分数学基础

微分的本质是一个微小的线性变化量，是用一个线性函数作为原函数变化的逼近。在机器学习中，微分计算实际上就是一系列有限的可微算子的组合。

链式法则

链式法则是微积分中的求导法则，用于求一个复合函数的导数，是在微积分的求导运算中一种常用的方法。自动微分的思想是将计算机程序中的运算操作分解为一个有限的基本操作集合，且集合中基本操作的求导规则均为已知。在完成每一个基本操作的求导后，使用链式法则将结果组合得到整体程序的求导结果。

\[f[g(h(x))]'=f'[g(h(x))]g'[h(x)]h'(x)\]

常见的求导方法

在机器学习中，反向传播不可或缺，是神经网络训练的中流砥柱。计算机中计算导数的方法主要可以分为以下四类：

1. 手动微分（manually differentiation）

   手动微分，顾名思义，即人为手动计算导数并编码。需要表达式为 closed-form 形式。

   优点：

   • 实现简单；
   • 结果准确；

   缺点：

   • 耗时长；
   • 易出错；
   • 通用性、灵活性差；

2. 数值微分（numerical differentiation）

   使用导数的定义 \(f'(x) = \frac {f(x+h)-f(x)}{h}\)，通过有限差分近似计算导数。强调一开始直接带入数值近似求解。

   优点：

   • 实现简单；
   • 适用性高；
   • 显式隐藏了求导过程；

   缺点：

   • 存在舍入和截断误差，结果不准确；
   • 对于梯度的扩展性很差，不适合参数量很大的模型；
   • 计算量大，每计算一个参数的导数，都需要重新计算，求解速度最慢；

3. 符号微分（symbolic differentiation）

   基于数学规则和程序表达式变换完成求导，其计算结果是导函数的表达式而非具体的数值。强调直接对代数进行求解，最后才代入数值问题。先求解析解，然后转换为程序，再通过程序计算出函数的梯度。需要表达式为 closed-form 形式。

   优点：

   • 变换过程中不涉及计算且是严格等价的，可以大大减小微分结果的误差；
   • 可用于类似极值的数学问题求解；

   缺点：

   • 表达式复杂时，会引入表达式膨胀的问题；

4. 自动微分（automatic differentiation）

   对于机器学习而言，不需要得到导数的表达式，只需要计算函数在某一点处的导数值。自动微分通过替换变量的域来合并导数值并重新定义运算符的语义以根据链式法则传播导数，采用类似有向图的计算来求解微分值。应用于最基本的算子，比如常数、幂函数、指数函数、对数函数、三角函数等，然后代入数值，保留中间结果，最后再应用于整个函数。

   缺点：

   • 需要存储一些中间结果求导，内存占用较大；

   优点：

   • 在代码执行期间累积值来计算导数以生成数值导数评估，只需要很小的常数开销；
   • 精度高，无表达式膨胀问题；

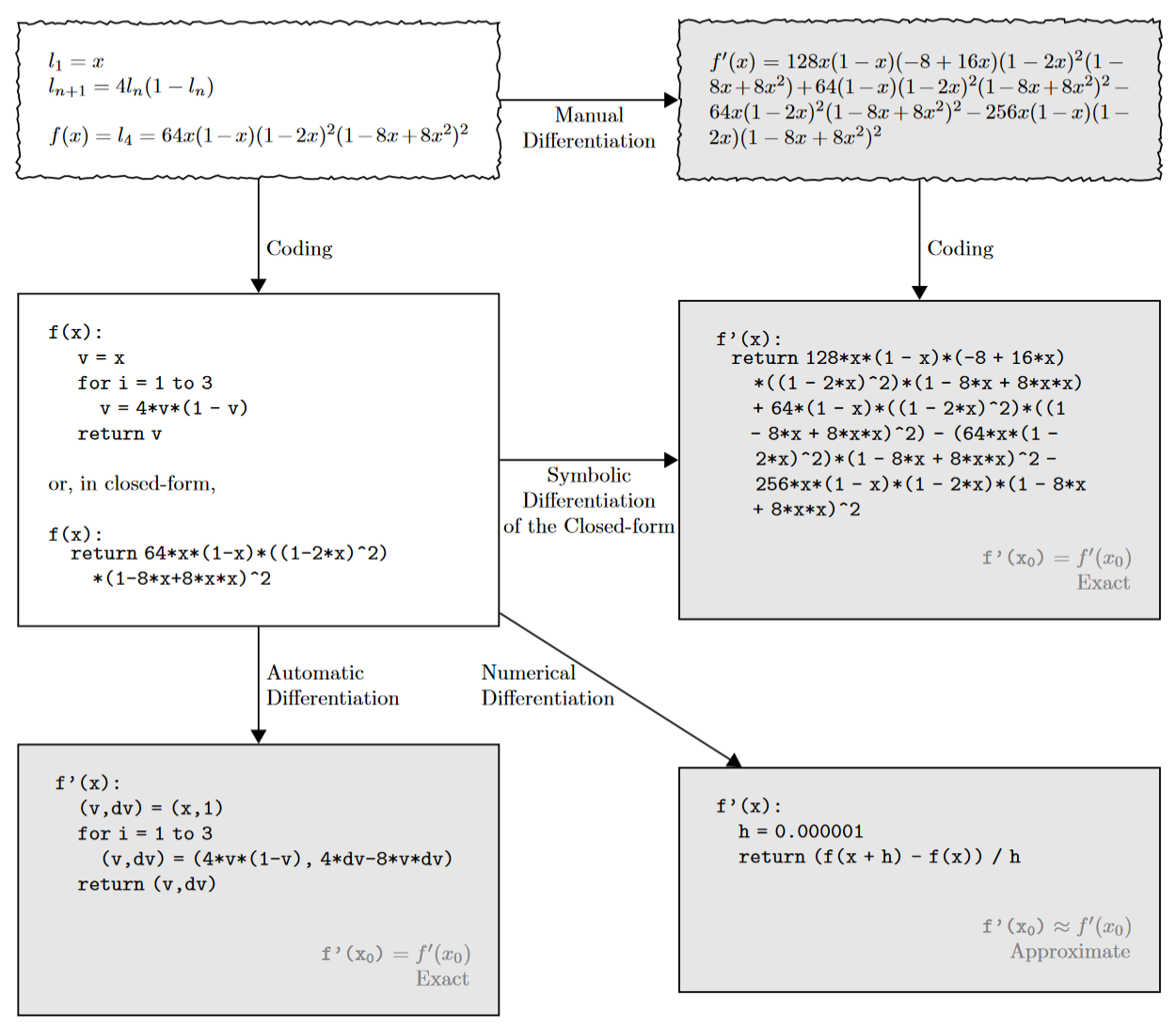
以左上角的表达式举例，手动微分（右上）需要手动对表达式求导；符号微分（右中）给出了精确的结果，但需要 closed-form 形式的输入，并且会受到表达式膨胀的影响；数值微分（右下）由于舍入和截断误差而存在精度问题；自动微分（左下）与符号微分一样准确，只需要常量开销并且支持控制流即可。

自动微分本质

一般我们可能会认为自动微分是一种数值微分或者符号微分，但实际上并不是这样的。自动微分提供了导数的数值，并且通过微分的符号规则来实现，因而它是介于数值微分和符号微分之间的一种方法。

自动微分法被认为是对计算机程序进行非标准的解释。自动微分基于一个事实，即每一个计算机程序，不论它有多么复杂，都是在执行加减乘除这一系列基本算数运算，以及指数、对数、三角函数这类初等函数运算。于是自动微分先将符号微分法应用于最基本的算子，比如常数，幂函数，指数函数，对数函数，三角函数等，然后代入数值，保留中间结果，最后再通过链式求导法则应用于整个函数。

通过将链式求导法则应用到这些运算上，我们能以任意精度自动地计算导数，而且最多只比原始程序多一个常数级的运算。

举个栗子，原始公式：

\[y=f(g(h(x)))=f(g(h(w_0)))=f(g(w_1))=f(w_2)=w_3\]

自动微分以链式法则为基础，把公式中一部分整理出来成为一些新变量，然后用这些新变量整体替换这个公式。

\[\begin{aligned} &w_0=x \\ &w_1=h(w_0) \\ &w_2=g(w_1) \\ &w_3=f(w_2)=y \\ \end{aligned}\]

然后把这些新变量作为节点，依据运算逻辑把公式整理出一张有向无环图。即原始函数建立计算图，数据正向传播，计算出中间节点 \(w_i\)，并记录计算图中的节点依赖关系。

因此，自动微分可以被认为是将一个复杂的数学运算过程分解为一系列简单的基本运算， 其中每一项基本运算都可以通过查表得出来。

自动微分的不同模式

自动微分分为正向模式（Forward Mode）和反向模式（Reverse Mode）两种。两种微分模式都通过递归的方式来求 \(dy / dx\)，只是根据链式法则展开的形式不太一样。

以计算图的方式表示基本运算的给定轨迹，可用于可视化中间变量之间的依赖关系，如下图，表示 \(f(x_1, x_2) = ln(x_1) + x_1x_2 - sin(x_2)\)：

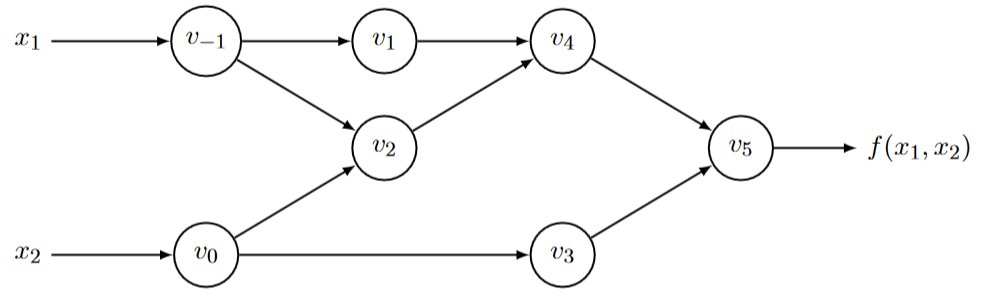
由于任何计算表达式值得代码都会产生具有输入、中间值和输出的求值轨迹，因此，自动微分不仅可以区分 closed-form 形式的表达式，还可以利用控制流算法，例如分支、循环、递归和过程调用。

雅可比（Jacobian）矩阵

在向量微积分中，Jacobian 矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为 Jacobian 行列式。Jacobian 矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。Jacobian 矩阵的第 i 行第 j 列元素为函数 i 对变量 j 的偏导数。Jacobian 矩阵表示两个向量所有可能的偏导数。它是一个向量相对于另一个向量的梯度，其实现的是 n 维向量 到 m 维向量的映射。

当有 n 个输入，m 个输出时，Jacobian 矩阵表示为：

\[J_f= \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \dots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \dots & \frac{\partial y_m}{\partial x_n} \\ \end{bmatrix}\]

正向模式（Forward Mode）

正向模式是自动微分中最简单的模式，正向梯度累积会指定从内到外的链式法则遍历路径，即先计算 \(dw_1/dx\)，再计算 \(dw_2/dw_1\)，最后计算 \(dy/dw_2\)，即正向模式是在计算图前向传播的同时计算微分，因此正向模式的一次正向传播就能计算出输出值和导数值。

\[\frac{dw_i}{dx}=\frac{dw_i}{dw_{i-1}} \frac{dw_{i-1}}{dx}\]

其中 \(\dot{v} =\frac{\partial v_i}{\partial x_1}\)，正向模式计算了雅可比矩阵的一列。

优点：

• 实现简单
• 不需要额外的内存空间

缺点：

• 每次只能对一个自变量的偏导数计算，对于一元函数求导是高效的，但是机器学习模型的入参数量及大，效率低；
• 如果函数由 n 个输入，m 个输出，对于每个输入来说，正向模式都需要遍历计算过程以得到当前输入的导数，求解整个函数的梯度需要 n 次上图的计算过程。

反向模式（Reverse Mode）

反向模式的自动微分对应于广义上的反向传播算法，因为它从给定输出向后传播导数。反向梯度累积会先计算 \(dy/dw_2\)，然后计算 \(dw_2/dw_1\)，最后计算 \(dw_1/dx\)。即，反向传播需要对计算图进行一次正向计算，得到输出值，再使用输出值进行反向传播。反向模式需要保存正向传播的中间变量值，这些中间变量值再反向传播的时候被用来计算导数，所以，反向传播的内存开销较大。

\[\frac{dy}{dw_i}=\frac{dy}{dw_{i+1}} \frac{dw_{i+1}}{dw_i}\]

其中 \(\overline{v} = \frac{\partial y_j}{\partial v_i}\)，反向模式计算了雅可比矩阵的一行。

优点：

• 通过一次反向计算，就可以计算出所有参数的偏导数，中间的偏导数只需计算一次；
• 减少了重复计算的工作量，再多参数的时候反向自动微分的时间复杂度更低；

缺点：

• 需要额外的数据结构记录正向过程的计算操作，用于反向使用；
• 带来了大量内存占用，为了减少内存操作，需要深度学习框架进行各种优化，也带来了额外的限制和副作用；

反向模式和正向模式是一对相反的过程，反向模式从最终结果开始求导，利用最终输出对每一个节点进行求导。

正向模式一次正向传播就能得到输出值的梯度，但是有 n 个输入就需要计算 n 次正向的流程。反向模式得到梯度需要先走一遍正向得到输出值，再通过输出值反向传播得到梯度，可以一次更新所有的参数，但需要记录中间变量值。

当输出维度小于输入维度时，反向模式的乘法次数小于正向模式，因此，当输出维度大于输入维度时，适宜使用正向模式微分；当输出维度远远小于输入的时候，适宜使用反向模式微分。

目前大部分AI框架都会优先采用反向模式，但是也有例如 MindSpore 等 AI 框架同时支持正反向的实现模式。在现今主流的自动微分框架 Pytorch 中，程序在执行的时候把计算图信息记录在一个叫做“张量”的变量中。每个张量都有一个叫做 tracker 的结构体在TensorFlow 中，用户必须在执行前构造静态图，而中间结果也被记录在这个静态图中。

自动微分的实现

在自动微分实现中的一个主要考虑因素是自动微分算数和轨迹追踪带来的性能开销。自动微分保证算术量的增加不超过一个小的常数因子。

自动微分的实现大致分为以下三类：

1. 基本表达式

   基本表达式法也叫做元素库（Elemental Libraries），程序中实现构成自动微分中计算的最基本的类别或者表达式，并通过调用自动微分中的库，来代替数学逻辑运算来工作。然后在函数定义中使用库公开的方法，这意味着在编写代码时，手动将任何函数分解为基本操作。

   该方法封装大多数的基本表达式及对应的微分表达式，通过库函数的方式提供给用户，用户在写代码时，需要手工分解程序为一系列的基本表达式，然后使用这些库函数去替换这些基本表达式。以 \(a=(x+y)/z\) 为例，用户需要手动把这个程序分解为：

    t = x + y
    a = t / z
   

   然后使用自动微分的库函数去替换分解出来的基本表达式：

    // 参数为变量x, y, t和对应的导数变量dx, dy, dt
    call ADAdd(x, dx, y, dy, t, dt)
    // 参数为变量t, z, a和对应的导数变量dt, dz, da
    call ADDiv(t, dt, z, dz, a, da)t = x + y
   

   库函数 ADAdd 和 ADDiv 运用链式法则，分别定义了 Add 和 Div 的微分表达式：

    def ADAdd(x, dx, y, dy, z, dz):
        z = x + y
        dz = dy + dx
   
    def ADDiv(x, dx, y, dy, z, dz):
        z = x / y
        dz = dx / y + (x / (y * y)) * dy
   

   优点：

   • 实现简单，基本可以在任意语言中快速地实现为库

   缺点：

   • 用户必须使用库函数进行编程，而无法使用语言原生地运算表达式
   • 实现逻辑和代码冗余较长，依赖于开发人员较强的数学背景

2. 操作符重载

   在具有多态特性的现代编程语言中，运算符重载提供了实现自动微分的最直接方式，利用了编程语言的第一特性（first class feature），重新定义了微分基本操作语义的能力。

   依赖于现代编程语言的多态特性，使用操作符重载对编程语言中的基本操作语义进行重定义，封装其微分规则。每个基本操作类型及其输入关系，在程序运行时会被记录在一个所谓的“tape”的数据结构里面，最后，这些“tape”会形成一个跟踪轨迹(trace)，我们就可以使用链式法则沿着轨迹正向或者反向地将基本操作组成起来进行微分。以自动微分库AutoDiff为例，对编程语言的基本运算操作符进行了重载：

    namespace AutoDiff
    {
        public abstract class Term
        {
        // 重载操作符 `+`，`*` 和 `/`，调用这些操作符时，会通过其中的
        // TermBuilder 将操作的类型、输入输出信息等记录至 tape 中
        public static Term operator+(Term left, Term right)
        {
            return TermBuilder.Sum(left, right);
        }
        public static Term operator*(Term left, Term right)
        {
            return TermBuilder.Product(left, right);
        }
        public static Term operator/(Term numerator, Term denominator)
        {
            return TermBuilder.Product(numerator, TermBuilder.Power(denominator, -1));
        }
        }
   
        // Tape 数据结构中的基本元素，主要包含：
        // 1) 操作的运算结果
        // 2) 操作的运算结果对应的导数结果
        // 3) 操作的输入
        // 除此外还通过函数 Eval 和 Diff 定义了该运算操作的计算规则和微分规则
        internal abstract class TapeElement
        {
        public double Value;
        public double Adjoint;
        public InputEdges Inputs;
   
        public abstract void Eval();
        public abstract void Diff();
        }
    }
   

   优点：

   • 利用编程语言第一特性，重新定义了微分基本操作语义的能力
   • 实现简单，只要求语言提供多态的特性能力
   • 易用性高，重载操作符后跟使用原生语言的编程方式类似

   缺点：

   • 需要显式构造特殊数据结构和对特殊数据结构进行大量的读写、遍历操作，这些额外数据结构和操作的引入不利于高阶微分的实现
   • 对于一些控制流表达式，难以通过操作符重载进行微分规则定义，对于这些操作的处理会退化成基本表达式方法中特定函数封装的方式，难以用原生的控制流表达式

3. 源代码变换

   源码转换（Source Code Transformation，SCT）是最复杂的，实现起来也是非常具有挑战性。

   源码转换的实现提供了对编程语言的扩展，可自动将算法分解为支持自动微分的基本操作。通常作为预处理器执行，以将扩展语言的输入转换为原始语言。简单来说就是利用源语言来实现领域扩展语言 DSL 的操作方式。

   其主要流程是：分析获得源程序的 AST 表达形式 -> 基于 AST 完成基本表达式的分解和微分操作 -> 遍历 AST 得到基本表达式间的依赖关系 -> 应用链式法则完成自动微分。

   优点：

   • 支持更多数据类型（原生和用户自定义的数据类型） + 原生语言操作（基本数学运算操作和控制流操作）
   • 高阶微分中实现容易，不用每次使用 Tape 来记录高阶的微分中产生的大量变量，而是统一通过编译器进行额外变量优化和重计算等优化
   • 进一步提升性能，能够对计算表达式进行统一的编译优化

   缺点：

   • 实现复杂，需要扩展语言的预处理器、编译器或解释器，深入计算机体系和底层编译
   • 支持更多数据类型和操作，用户自然度虽然更高，但更容易写出不支持的代码导致错误
   • 微分结果以代码形式存在，不利于深度调试

参考链接

1. Automatic Differentiation in Machine Learning: a Survey
2. 知乎专栏：自动微分(Automatic Differentiation)
3. openmlsys